..Sedikit Catatan tentang Hidup..

Pendugaan Nilai π (phi)

Dalam perhitungan matematika, kita seringkali menggunakan bilangan dengan simbol π. Bilangan ini digunakan untuk perhitungan bangun datar lingkaran. Misalnya untuk mencari luas lingkaran dan keliling lingkaran.
Sejak pertama kali dikenalkan kepada kita ketika masih berada di sekolah dasar, nilai π ini diasumsikan sama dengan atau 3,14. Dimana kedua nilai ini merupakan bilangan rasional (bilangan yang dapat diubah ke dalam bentuk pecahan).
Namun, ternyata setelah dipelajari lebih lanjut, ternyata nilai π ini bukan merupakan bilangan rasional. Untuk bisa menduga berapa sebenarnya nilai dari bilangan π.
Untuk menduga nilai π ini, kita bisa menggunakan cara berpikir yang sederhana sebelum kita menuangkannya dalam bentuk program computer.
Misalkan saja dalam sebuah papan tulis hitam (blackboard), kita menggambarkan sebuah persegi yang didalamnya berisi sebuah lingkaran dan lingkaran tersebut menyinggung sisi dari persegi. Dengan kata lain, sisi persegi = diameter lingkaran. Untuk lebih jelasnya bisa dilihat pada gambar berikut :



Dari kejauhan kita melemparkan kapur tulis ke papan tulis selama n kali. Kemudian bisa hitung berapa kapur yang jatuh pada lingkaran (m) dan yang jatuh pada persegi (n). Dari nilai m dan n yang didapatkan ini, bisa diperoleh nilai π dengan menggunakan persamaan: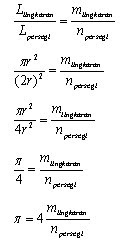


Jika persamaan tersebut kita terjemahkan dalam bahasa pemograman dengan algoritma :
1. Mulai
2. i = 0
3. i = i+1
4. Bangkitkan 1000 titik
x ~ U(0,1)
y ~ U(0,1)
5. π = 4*(m/n)
6. jika i<1000 pergi ke 3
7.

8. Tulis π
9. Selesai

Sebagai orang Statistika, sering sekali kita mendengar kata varians. Dalam Statistika, rumus varians yang diambil dalam sampel berbeda dengan nilai varians dalam populasi. Hal ini karena sampel masih merupakan dugaan dari populasi, jadi bisa saja nilai varians sampel berbeda dengan nilai varians populasi. Jika kita ingin bisa melihat perbedaan dan bias yang dimiliki kedua varians tersebut, kita bisa menggunakan algoritma seperti di bawah ini :
1. Mulai
2. Bangkitkan data x ~ N(60,1) sebanyak 100 sebagai populasi
3.Ambil n sampel sebanyak 10
Hitung :

4. Lakukan 3 sebanyak 1000 kali
5. Hitung bias S12 dan S22 dan bandingkan
6. Selesai